Kreise, die auf Kreisen kreisen
Hier gibt es Bilder zu den Formeln
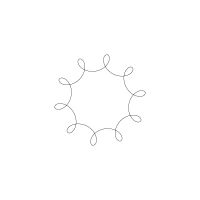
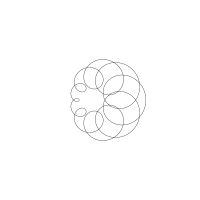
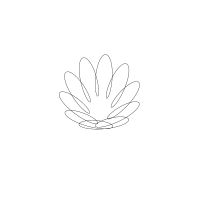
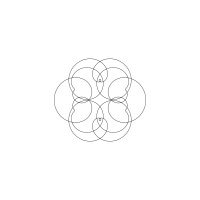
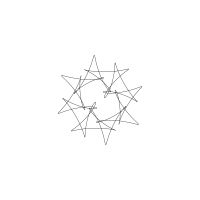
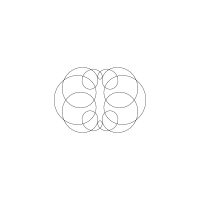
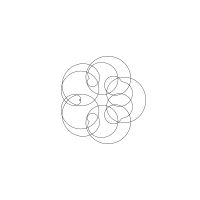
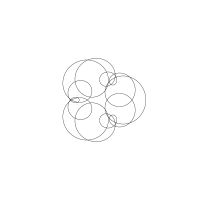
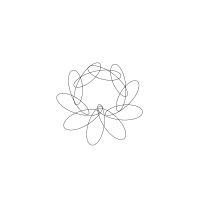
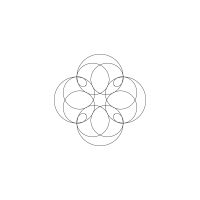
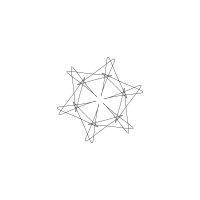
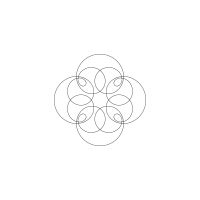
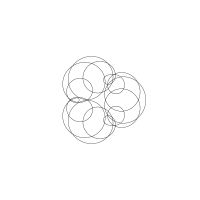
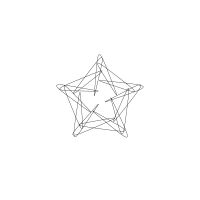
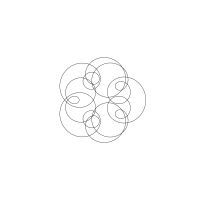
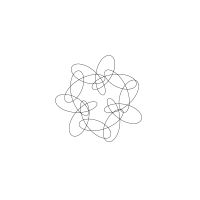
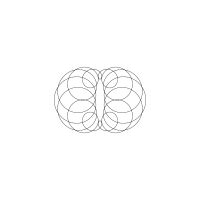
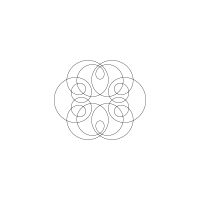
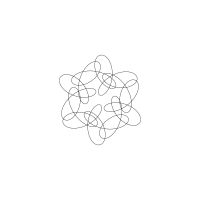
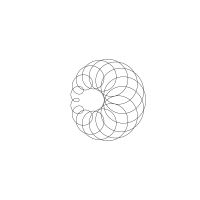
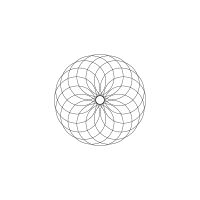
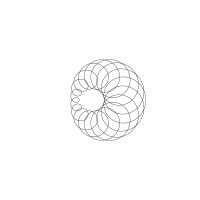
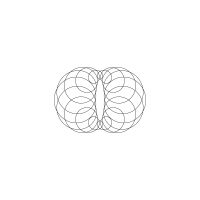
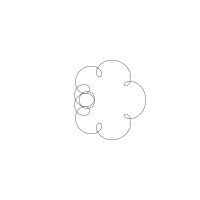
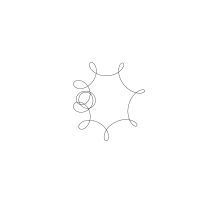
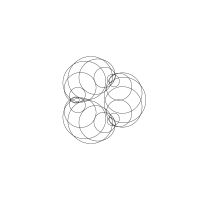
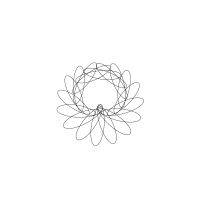
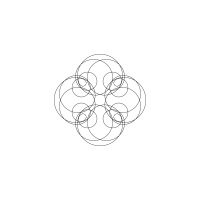
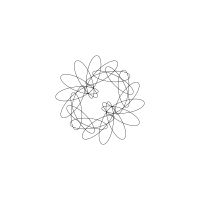
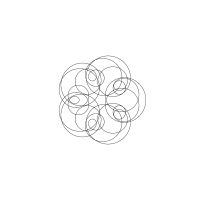
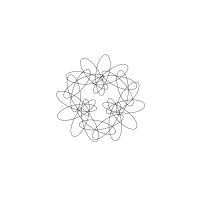
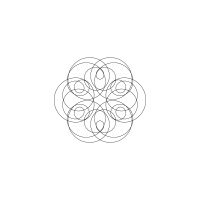
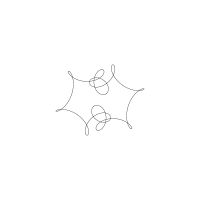
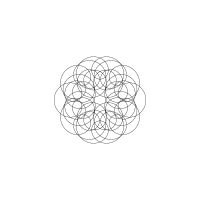
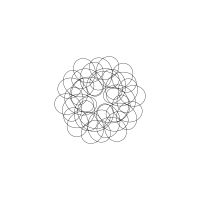
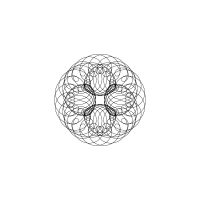
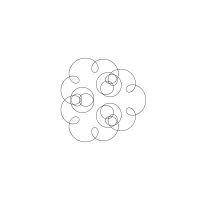
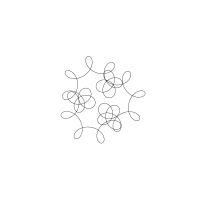
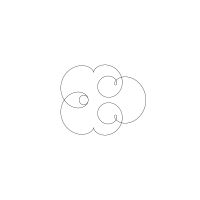
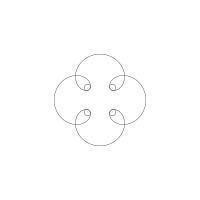
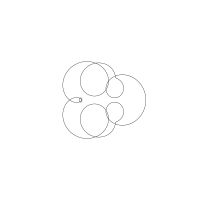
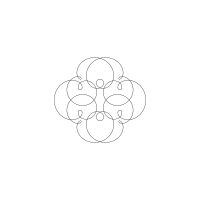
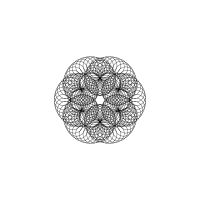
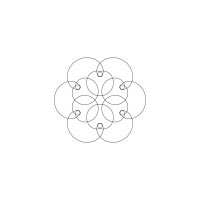
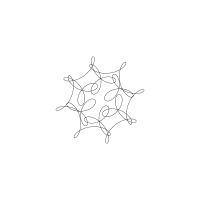
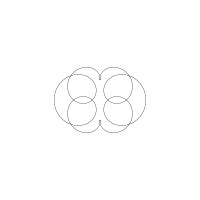
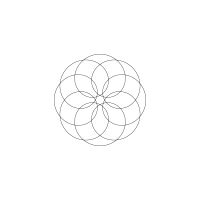
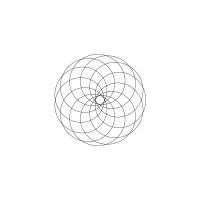
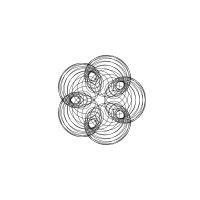
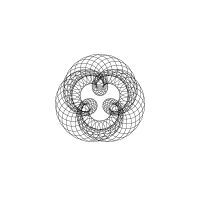
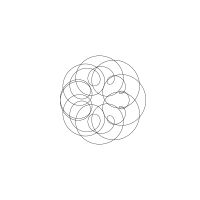
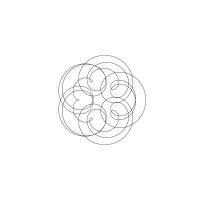
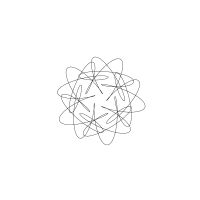
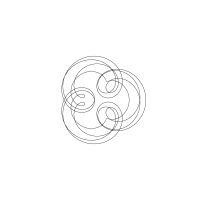
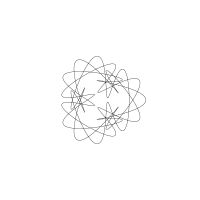
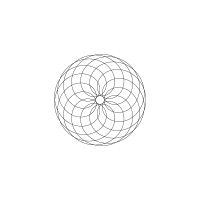
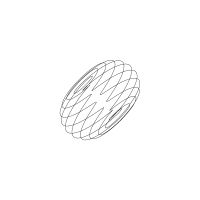
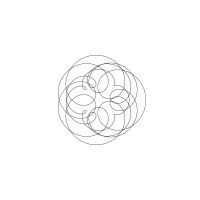
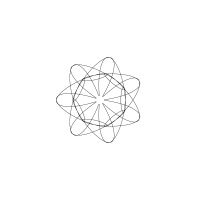
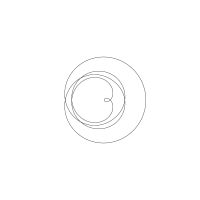
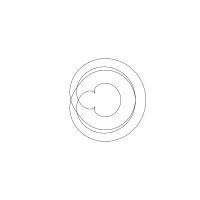
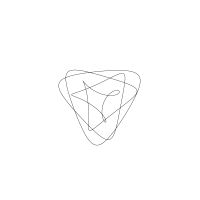
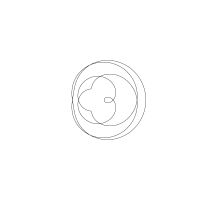
1/u (cos(at),sin(at)) + 1/v (cos(bt),sin(bt)) + 1/w (cos(ct),sin(ct))
oder
1/u (cos(at),sin(at)) + 1/v (cos(bt),sin(bt)) + 1/w (sin(ct),cos(ct))
Unter jedem Bild steht die Folge u_v_w_a_b_c (für die erste Formel) und u_v_w_a_b_c_ (für die zweite Formel).
Siehe auch
H.R. Schneebeli, H.R. Vollmer: Kreise, die auf Kreisen kreisen
A. Wassermann: Interaktive Visualisierung mit JSXGraph