Using this program it is possible to
The following tables were found in a paper by Franck Jedrzejewski: They show the GAP-index of the serial group in the list of all 301 transitive groups on {1,…,12}, the order of the group, the numbers of chord diagrams which yield this serial group, and some information on the block types of these groups.
| r | |G| | Chord diagrams | Blocks |
| 12 | 24 | 358,554 | B1 |
| 28 | 48 | 444,509 | B1 |
| 54 | 96 | 186 | B2 |
| 81 | 144 | 1,381, 553 | B3 |
| 86 | 192 | 491,549 | B3 |
| 118 | 216 | 50,359, 474 | B4 |
| 125 | 288 | 487 | B3 |
| 151 | 384a | 414 | B6 |
| 152 | 384b | 383,497,507,508 | B6 |
| 154 | 384c | 136,536 | B2 |
| 156 | 432 | 248 | B4 |
| 185 | 768a | 157,552 | B6 |
| 186 | 768b | 348,530 | B6 |
| 193 | 768c | 490 | B2 |
| 217 | 1296 | 247,516 | B4 |
| 218 | 1320 | 103,161,184,241,395,417,448,510 | |
| 240 | 2304 | 43,351,440,537 | B5 |
| 248 | 2592 | 364 | B4 |
| 260 | 4608 | 544 | B5 |
| 267 | 5184 | 11,282,303 | B8 |
| 270 | 7680 | 42,61,111,347,355,382,412,441,504,538,551 | B9 |
| 288 | 28800 | 24,51,56,150,163,183,252,332,371,376,419,420,439,481,514 | B7 |
| 293 | 46080 | 109,185,346,350,357,488,531,535,546,550 | B9 |
| 294 | 82944 | 170,174,285,289,313,321 | B8 |
| 299 | 1036800 | 3,6,7,26,31,34,36,60,137,142,153,155,168,181,188,190,207,209,281, | B7 |
| 290,295,305,334,352,362,418,434,482,494,511,532 | |||
| 301 | 479001600 | 431 remaining chord diagrams | |
The Block Systems for the serial groups are
| B1 | = | [ 1, 3, 5, 7, 9, 11 ], [ 1, 4, 7, 10 ], [ 1, 5, 9 ], [ 1, 7 ] |
| B2 | = | [ 1, 3, 5, 7, 9, 11 ], [ 1, 4, 7, 10 ], [ 1, 7 ] |
| B3 | = | [ 1, 3, 5, 7, 9, 11 ], [ 1, 5, 9 ], [ 1, 7 ] |
| B4 | = | [ 1, 3, 5, 7, 9, 11 ], [ 1, 5, 9 ] |
| B5 | = | [ 1, 3, 5, 7, 9, 11 ], [ 1, 7 ] |
| B6 | = | [ 1, 4, 7, 10 ], [ 1, 7 ] |
| B7 | = | [ 1, 3, 5, 7, 9, 11 ] |
| B8 | = | [ 1, 4, 7, 10 ] |
| B9 | = | [ 1, 7 ] |
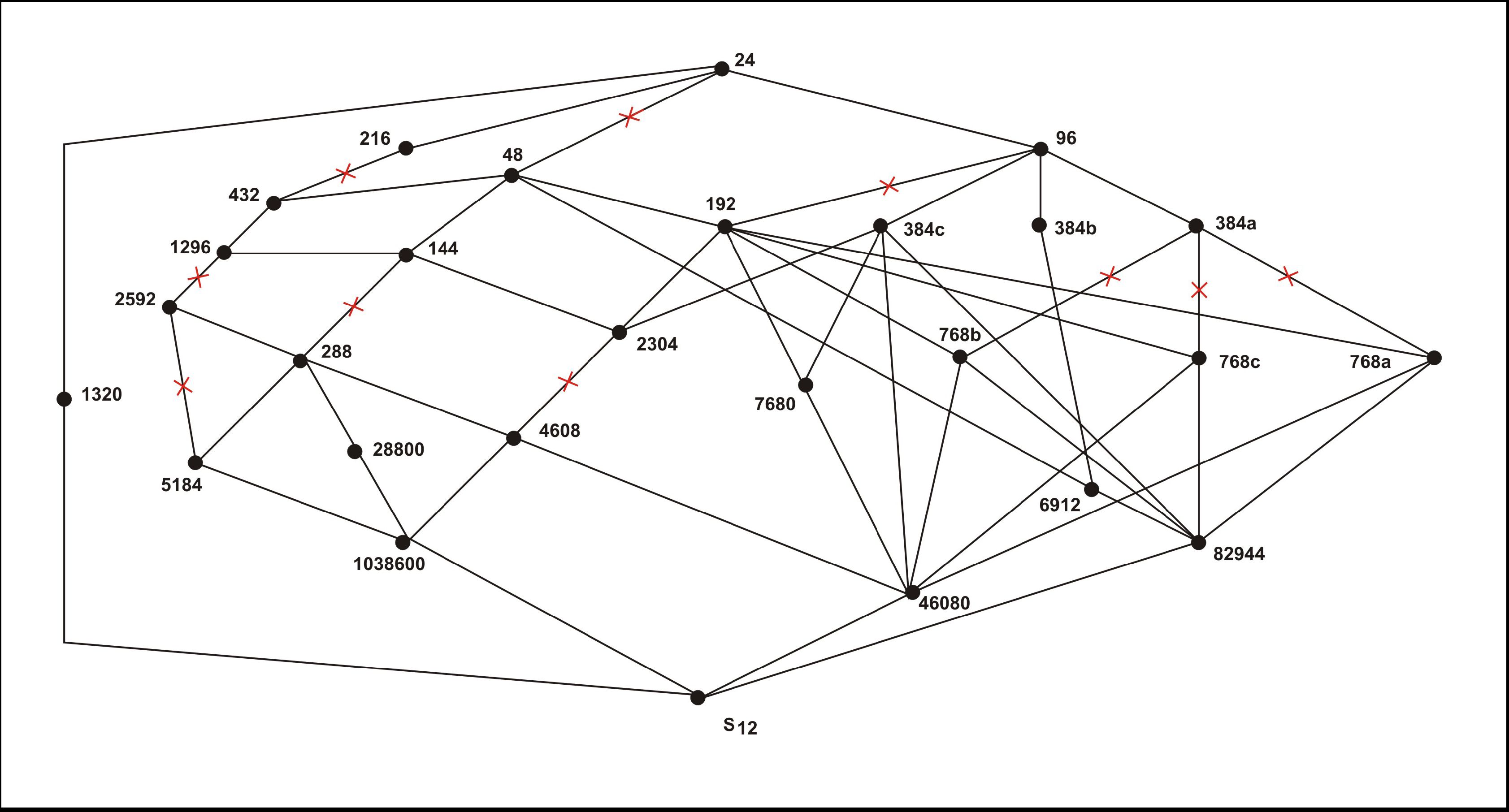
This is the lattice of the 26 serial groups computed by Franck Jedrzejewski. The groups are represented by their order. A red cross on a line connecting two groups indicates that the smaller group is a normal subgroup in the bigger one.
